Tag: Proof

Iterative Methods: Part 2

Last time, we looked at 2D Poisson’s equation and discussed how to arrive at a matrix equation using the finite difference method. The matrix, which represents the discrete Laplace operator, is sparse, so we can use an iterative method to solve the equation efficiently.

Today, we will look at Jacobi, Gauss-Seidel, Successive Over-Relaxation (SOR), and Symmetric SOR (SSOR), and a couple of related techniques—red-black ordering and Chebyshev acceleration. In addition, we will analyze the convergence of each method for the Poisson’s equation, both analytically and numerically.

Continue reading “Iterative Methods: Part 2”

Iterative Methods: Part 1

Once again, we consider solving the equation 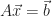A\vec{x} = \vec{b}, where A \in \mathbb{R}^{n \times n} is nonsingular. When we use a factorization method for dense matrices, such as LU, Cholesky, SVD, and QR, we make 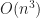O(n^{3}) operations and store O(n^{2}) matrix entries. As a result, it’s hard to accurately model a real-life problem by adding more variables.

Luckily, when the matrix is sparse (e.g. because we used finite difference method or finite element method), we can use an iterative method to approximate the solution efficiently. Typically, an iterative method incurs O(n^{2}) operations, if not fewer, and requires O(n) storage.

Over the next few posts, we will look at 5 iterative methods:

  • Jacobi
  • Gauss-Seidel
  • Successive Over-Relaxation (SOR)
  • Symmetric SOR (SSOR)
  • Conjugate Gradient (CG).

In addition, we will solve 2D Poisson’s equation using these methods. We will compare the approximate solutions to the exact to illustrate the accuracy of each method.

Continue reading “Iterative Methods: Part 1”

Hearing Perturbation Theory

In numerical linear algebra, we create ways for a computer to solve a linear system of equations A\vec{x} = \vec{b}. In doing so, we analyze how efficiently and accurately we can find the solution \vec{x}.

Perturbation theory concerns how much error we incur in the solution \vec{x} when we perturb (spoil) the data A and \vec{b}. A classic statement tells us that the amount of error depends on the condition number of the matrix A.

I will define and prove the statement, and help you understand it by “hearing” it.

Continue reading “Hearing Perturbation Theory”

Monte Carlo Simulations: Buffon’s Needle

Buffon’s needle is a classic Monte Carlo simulation that we can conduct in a classroom. We give the students, say 10 needles each, and have them drop the needles on a paper that we provide also. The paper is special, in that it has parallel lines that are separated by the length of a needle. Each student records how many needles intersect one of the lines, then we tally their numbers to arrive at a very special number. (Guess who?)

In a class of 30, we have 300 samples to determine this special number. If the students had repeated the experiment ten times (any more than this risks frustration and wrath), we would have 3,000 samples at best. But with a computer program, we can make a million samples easily. In less than a second!

So today, we will learn how to write a program that generates needles (line segments). Our program needs to determine if a needle intersects a line. In general, checking if two line segments intersect is not an easy task. It’s rather amazing how we can look at many line segments (like the ones in the picture above) and instantly tell which lines intersect with which others. In our problem, fortunately, the lines on the paper are parallel and are equally spaced apart. We can use this fact to come up with a simple solution. Lastly, we will learn how to vectorize our code. Vectorization allows us to arrive at the answer quickly.

Continue reading “Monte Carlo Simulations: Buffon’s Needle”

Monte Carlo Simulations: Penney’s Game

An n-gram is a word of length n that we can create from a set of letters. With two letters \{\mbox{T}, \mbox{H}\}, we can form these 3-grams: \mbox{TTT}, \mbox{TTH}, \mbox{THT}, \mbox{THH}, \mbox{HTT}, \mbox{HTH}, \mbox{HHT}, and \mbox{HHH}. We will let \mbox{T} stand for tails and \mbox{H} for heads, so that a 3-gram can represent an outcome if we flip a coin 3 times.

Penney’s game concerns two good friends and their n-grams. The game is simple and seemingly fair. Soon Player 1 will call off their long friendship and leave, however. We will find that, whenever n \geq 3, Player 2 is always more likely to win.

Continue reading “Monte Carlo Simulations: Penney’s Game”