Let’s look at one more way to solve the equation $A\vec{x} = \vec{b}$ . We assume that $A \in \mathbb{R}^{n \times n}$ is nonsingular, and define the $k$ -th Krylov subspace as follows:

$\mathscr{K}_{k} \,:=\, \mbox{span}\{\vec{b},\,A\vec{b},\,\cdots,\,A^{k - 1}\vec{b}\}$ .

Krylov subspace methods are efficient and popular iterative methods for solving large, sparse linear systems. When $A$ is symmetric, positive definite (SPD), i.e.

$\left\{\begin{array}{l} A^{T} = A \\[12pt] \vec{x}^{T}A\vec{x} > 0,\,\,\,\forall\,\vec{x} \neq \vec{0}, \end{array}\right.$

we can use a Krylov subspace method called Conjugate Gradient (CG).

Today, let’s find out how CG works and use it to solve 2D Poisson’s equation.

4. Conjugate Gradient

a. Creating iterates

Let $(\cdot,\,\cdot)$ be an inner product for $\mathbb{R}^{n}$ , and $||\cdot|| := \sqrt{(\cdot,\,\cdot)}$ the norm associated with the inner product.

How Krylov subspace methods work is simple. We will approximate the exact solution $\vec{x} = A^{-1}\vec{b}$ with a sequence of iterates $\vec{x}_{k}$ that meet two conditions:

$\begin{array}{l} \mbox{1.}\,\,\,\vec{x}_{k} \in \mathscr{K}_{k} \\[12pt] \mbox{2.}\,\,\,||\vec{x}_{k} - \vec{x}|| = \min\limits_{\vec{y}\,\in\,\mathscr{K}_{k}}\,||\vec{y} - \vec{x}||.\end{array}$

In other words, when measured in the norm $||\cdot||$ , $\vec{x}_{k}$ is the best approximation to $\vec{x}$ from the $k$ -th Krylov subspace.

(For initialization, we will take $\vec{x}_{0} = \vec{0}$ and $\mathscr{K}_{0} = \{\vec{0}\}$ .)

The optimality condition above is the same as the orthogonality condition $\vec{x}_{k} - \vec{x} \perp \mathscr{K}_{k}$ under the inner product $(\cdot,\,\cdot)$ . Therefore, $\vec{x}_{k}$ satisfies the equation,

$(\vec{x}_{k} - \vec{x},\,\vec{y}) = 0,\,\,\,\forall\,\vec{y} \in \mathscr{K}_{k}$ .

Lemma 1.

The orthogonality condition and the fact that $\mathscr{K}_{k - 1} \subset \mathscr{K}_{k}$ imply two things. At every iteration $k \geq 1$ ,

$\begin{array}{l} \mbox{1.}\,\,\,\vec{x}_{k} - \vec{x}_{k - 1} \in \mathscr{K}_{k} \\[12pt] \mbox{2.}\,\,\,\vec{x}_{k} - \vec{x}_{k - 1} \perp \mathscr{K}_{k - 1}.\end{array}$

Proof.

First, note that the vector

$\vec{x}_{k} - \vec{x}_{k - 1} \,\equiv\, (\vec{x}_{k} - \vec{x}) - (\vec{x}_{k - 1} - \vec{x})$

represents the decrease in error over 1 iteration.

Since $\vec{x}_{k} \in \mathscr{K}_{k}$ and $\vec{x}_{k - 1} \in \mathscr{K}_{k - 1} \subset \mathscr{K}_{k}$ , we know that $\vec{x}_{k} - \vec{x}_{k - 1} \in \mathscr{K}_{k}$ .

Furthermore, for any $\vec{y} \in \mathscr{K}_{k - 1}\,(\subset \mathscr{K}_{k})$ ,

$(\vec{x}_{k} - \vec{x}_{k - 1},\,\vec{y}) \,=\, \underbrace{(\vec{x}_{k} - \vec{x},\,\vec{y})}_{=\,0} \,-\, \underbrace{(\vec{x}_{k - 1} - \vec{x},\,\vec{y})}_{=\,0} \,=\, 0.$

■

b. Creating residuals

Next, we select a vector $\vec{p}_{k} \neq \vec{0}$ that meets these conditions:

$\begin{array}{l} \mbox{1.}\,\,\,\vec{p}_{k} \in \mathscr{K}_{k} \\[12pt] \mbox{2.}\,\,\,\vec{p}_{k} \perp \mathscr{K}_{k - 1}.\end{array}$

(For initialization, we will take $\vec{p}_{1} = \vec{b}$ .)

The vector $\vec{x}_{k} - \vec{x}_{k - 1}$ also satisfied these conditions, so the two are linearly dependent. There is some constant $\alpha_{k} \in \mathbb{R}\,\backslash\,\{0\}$ such that $\vec{x}_{k} - \vec{x}_{k - 1} = \alpha_{k}\vec{p}_{k}$ .

We now have a way to compute the best approximation $\vec{x}_{k}$ from the previous one:

$\boxed{\vec{x}_{k} = \vec{x}_{k - 1} + \alpha_{k}\vec{p}_{k},\,\,\,\forall\,k \geq 1}$ .

This holds, provided we have a search direction $\vec{p}_{k}$ .

Lemma 2.

The coefficient $\alpha_{k}$ is given by,

$\boxed{\displaystyle\alpha_{k} = -\frac{(\vec{x}_{k - 1} - \vec{x},\,\vec{p}_{k})}{(\vec{p}_{k},\,\vec{p}_{k})} = \frac{(A^{-1}\vec{r}_{k - 1},\,\vec{p}_{k})}{(\vec{p}_{k},\,\vec{p}_{k})},\,\,\,\forall\,k \geq 1}$ ,

where $\vec{r}_{k} := \vec{b} - A\vec{x}_{k}$ is the residual.

Proof.

We have the equation,

$\vec{x}_{k} - \vec{x} = (\vec{x}_{k - 1} - \vec{x}) + \alpha_{k}\vec{p}_{k}$ .

On each side, take the inner product with $\vec{p}_{k}$ :

$(\vec{x}_{k} - \vec{x},\,\vec{p}_{k}) = (\vec{x}_{k - 1} - \vec{x},\,\vec{p}_{k}) + \alpha_{k}(\vec{p}_{k},\,\vec{p}_{k})$ .

Since $\vec{x}_{k} - \vec{x} \perp \mathscr{K}_{k}$ and $\vec{p}_{k} \in \mathscr{K}_{k}$ , the LHS is equal to 0. Hence,

$\displaystyle\alpha_{k} = -\frac{(\vec{x}_{k - 1} - \vec{x},\,\vec{p}_{k})}{(\vec{p}_{k},\,\vec{p}_{k})}$ .

Note, $\vec{r}_{k - 1} = A(\vec{x} - \vec{x}_{k - 1})$ .

■

Lemma 3.

The residuals are related in the following manner:

$\boxed{\vec{r}_{k} = \vec{r}_{k - 1} - \alpha_{k}A\vec{p}_{k},\,\,\,\forall\,k \geq 1}$ .

Proof.

Apply $A$ to both sides of the equation:

$(\vec{x} - \vec{x}_{k}) = (\vec{x} - \vec{x}_{k - 1}) - \alpha_{k}\vec{p}_{k}$ .

■

c. Creating search directions

We will now construct the search direction $\vec{p}_{k + 1}$ so that we can continue the iteration. Along the way, we required the search directions to satisfy,

$\vec{p}_{i} \in \mathscr{K}_{i} \,\backslash\, \{\vec{0}\} \,\,\,\mbox{and}\,\,\,\vec{p}_{i} \perp \mathscr{K}_{i - 1},\,\,\,\forall\,i = 1,\,\cdots,\,k$ .

Thus, if $\vec{p}_{k + 1}$ also meets these conditions, namely,

$\vec{p}_{k + 1} \in \mathscr{K}_{k + 1} \,\backslash\, \{\vec{0}\} \,\,\,\mbox{and}\,\,\,\vec{p}_{k + 1} \perp \mathscr{K}_{k}$ ,

then $\{\vec{p}_{1},\,\cdots,\,\vec{p}_{k + 1}\}$ will end up forming an orthogonal basis for $\mathscr{K}_{k + 1}$ .

We can create such a sequence using Gram-Schmidt method! Specifically, $\vec{p}_{k + 1}$ will be the sum of a vector in $\mathscr{K}_{k}$ (which can be written as a linear combination of $\vec{p}_{1},\,\cdots,\,\vec{p}_{k}$ ) and an offshoot $\vec{w}_{k} \in \mathscr{K}_{k + 1} \,\backslash\, \mathscr{K}_{k}$ :

$\boxed{\displaystyle\vec{p}_{k + 1} = \vec{w}_{k} + \sum_{i\,=\,1}^{k}\,\gamma_{i}\vec{p}_{i},\,\,\,\forall\,k \geq 1}$ .

Then, we orthogonalize $\vec{p}_{k + 1}$ against $\vec{p}_{1},\,\cdots,\,\vec{p}_{k}$ .

Lemma 4.

In the $k$ -th iteration, the coefficients $\gamma_{i}$ are given by,

$\boxed{\displaystyle\gamma_{i} = -\frac{(\vec{w}_{k},\,\vec{p}_{i})}{(\vec{p}_{i},\,\vec{p}_{i})},\,\,\,\forall\,i = 1,\,\cdots,\,k}$ .

Proof.

Given the equation,

$\displaystyle\vec{p}_{k + 1} = \vec{w}_{k} + \sum_{j\,=\,1}^{k}\,\gamma_{j}\vec{p}_{j}$ ,

we can take the inner product with $\vec{p}_{i}$ :

$\displaystyle(\vec{p}_{k + 1},\,\vec{p}_{i}) = (\vec{w}_{k},\,\vec{p}_{i}) + \sum_{j\,=\,1}^{k}\,\gamma_{j}(\vec{p}_{j},\,\vec{p}_{i})$ .

Since $\vec{p}_{k + 1} \perp \mathscr{K}_{i}$ and $\vec{p}_{i} \in \mathscr{K}_{i}$ , the LHS is equal to 0. Furthermore, $\{\vec{p}_{1},\,\cdots,\,\vec{p}_{k}\}$ forms an orthogonal basis, so the summation on the RHS reduces to a single term:

$\displaystyle\sum_{j\,=\,1}^{k}\,\gamma_{j}(\vec{p}_{j},\,\vec{p}_{i}) = \gamma_{i}(\vec{p}_{i},\,\vec{p}_{i})$ .

We can now solve for $\gamma_{i}$ :

$\displaystyle\gamma_{i} = -\frac{(\vec{w}_{k},\,\vec{p}_{i})}{(\vec{p}_{i},\,\vec{p}_{i})}$ .

■

Isn’t it cool to work backwards and see the motivations? We just need to figure out how to choose $\vec{w}_{k} \in \mathscr{K}_{k + 1} \,\backslash\, \mathscr{K}_{k}$ .

d. SPD

So far, we have not used the fact that $A$ is SPD. We do so now to obtain CG.

Lemma 5.

If $A \in \mathbb{R}^{n \times n}$ is SPD, then

$(\vec{x},\,\vec{y})_{A} := \vec{x}^{T}A\vec{y}$

defines an inner product for $\mathbb{R}^{n}$ . Then, $||\vec{x}||_{A} := \sqrt{(\vec{x},\,\vec{x})_{A}}$ gives us a norm, called the $A$ -norm.

Proof.

Let’s show that, for all vectors $\vec{x},\,\vec{y},\,\vec{z} \in \mathbb{R}^{n}$ and scalars $\alpha,\,\beta \in \mathbb{R}$ , the $A$ -inner product is symmetric, bilinear, and positive-definite:

Symmetric:

$\begin{aligned} (\vec{x},\,\vec{y})_{A} &= \vec{x}^{T}A\vec{y} \\[12pt] &= \vec{x}^{T}A^{T}\vec{y} \\[12pt] &= (A\vec{x})^{T}\vec{y} \\[12pt] &= \vec{y}^{T}(A\vec{x}) \\[12pt] &= (\vec{y},\,\vec{x})_{A}. \end{aligned}$

Notice how we used symmetry of the Euclidean inner product.

Bilinear:

$\begin{aligned} (\alpha\vec{x} + \beta\vec{y},\,\vec{z})_{A} &= (\alpha\vec{x} + \beta\vec{y})^{T}A\vec{z} \\[12pt] &= \alpha(\vec{x}^{T}A\vec{z}) + \beta(\vec{y}^{T}A\vec{z}) \\[12pt] &= \alpha(\vec{x},\,\vec{z})_{A} + \beta(\vec{y},\,\vec{z})_{A}. \end{aligned}$

Since the $A$ -inner product is symmetric, we also have linearity in the second argument.

Positive-definite:

Because $A$ is positive definite,

$(\vec{x},\,\vec{x})_{A} = \vec{x}^{T}A\vec{x} > 0,\,\,\,\forall\,\vec{x} \neq \vec{0}$ .

The $A$ -inner product is equal to zero only when $\vec{x} = \vec{0}$ .

■

The key thing to realize is that Sections 4a – 4c are valid for any nonsingular matrix $A$ . We can create a Krylov subspace method even if $A$ is not positive definite, or even symmetric. We just need to define an inner product and select $\vec{w}_{k}$ appropriately.

Let’s summarize what we learned so far using the $A$ -inner product.

We want to arrive at the solution $\vec{x}$ by a sequence of best approximations $\vec{x}_{k}$ . Best approximations satisfy the orthogonality condition:

$(\vec{x}_{k} - \vec{x},\,\vec{y})_{A} = 0,\,\,\,\forall\,\vec{y} \in \mathscr{K}_{k}$ .

By sheer luck (or well-planning), the residual $\vec{r}_{k}$ is orthogonal to the Krylov subspace $\mathscr{K}_{k}$ in the Euclidean inner product:

$(\vec{r}_{k},\,\vec{y})_{E} = (\vec{x} - \vec{x}_{k},\,\vec{y})_{A} = 0,\,\,\,\forall\,\vec{y} \in \mathscr{K}_{k}$ .

In particular, this means the residuals are orthogonal to each other. Hence the name Conjugate Gradient (“orthogonal residuals” didn’t sound good).

Given a best approximation $\vec{x}_{k - 1} \in \mathscr{K}_{k - 1}$ , we can find the next one $\vec{x}_{k} \in \mathscr{K}_{k}$ :

$\vec{x}_{k} = \vec{x}_{k - 1} + \alpha_{k}\vec{p}_{k}$ ,

where,

$\displaystyle\alpha_{k} = \frac{(A^{-1}\vec{r}_{k - 1},\,\vec{p}_{k})_{A}}{(\vec{p}_{k},\,\vec{p}_{k})_{A}} = \frac{\vec{r}_{k - 1}^{T}\vec{p}_{k}}{\vec{p}_{k}^{T}A\vec{p}_{k}}$ .

We can also find the residual:

$\vec{r}_{k} = \vec{r}_{k - 1} - \alpha_{k}A\vec{p}_{k}$ .

Notice that $A\vec{p}_{k}$ appeared again. It’d be nice to implement a sparse matrix-vector multiplication and store this result.

To continue the iteration, we decide on a search direction for some $\vec{w}_{k}$ :

$\displaystyle\vec{p}_{k + 1} = \vec{w}_{k} + \sum_{i\,=\,1}^{k}\,\gamma_{i}\vec{p}_{i}$ ,

where,

$\displaystyle\gamma_{i} = -\frac{(\vec{w}_{k},\,\vec{p}_{i})_{A}}{(\vec{p}_{i},\,\vec{p}_{i})_{A}} = -\frac{\vec{w}_{k}^{T}A\vec{p}_{i}}{\vec{p}_{i}^{T}A\vec{p}_{i}}$ .

e. Creating offshoots

There are a few candidates for $\vec{w}_{k} \in \mathscr{K}_{k + 1}\,\backslash\,\mathscr{K}_{k}$ . We will select the residual,

$\boxed{\vec{w}_{k} = \vec{r}_{k}}$ ,

so that all but one of the coefficients $\gamma_{i}$ will be 0!

Lemma 6.

When $\vec{w}_{k} = \vec{r}_{k}$ ,

$(\vec{w}_{k},\,\vec{p}_{i})_{A} = 0,\,\,\,\forall\,i = 1,\,\cdots,\,(k - 1)$ .

Proof.

First, let’s check that $\vec{r}_{k} \in \mathscr{K}_{k + 1} \,\backslash\, \mathscr{K}_{k}$ .

We know that the residual $\vec{r}_{k}$ resides in $\mathscr{K}_{k + 1}$ , because $\vec{b} \in \mathscr{K}_{k + 1}$ (by definition of the Krylov subspace) and $\vec{x}_{k} \in \mathscr{K}_{k}$ implies $A\vec{x}_{k} \in \mathscr{K}_{k + 1}$ .

Moreover, $\vec{r}_{k}$ is orthogonal to $\mathscr{K}_{k}$ in the Euclidean inner product, so $\vec{r}_{k} \not\in \mathscr{K}_{k}$ . By the same token,

$(\vec{r}_{k},\,\vec{p}_{i})_{A} = (\vec{r}_{k},\,A\vec{p}_{i})_{E} = 0,\,\,\,\forall\,i = 1,\,\cdots,\,(k - 1).$

■

Lemma 7.

When $\vec{w}_{k} = \vec{r}_{k}$ , we can simplify the formulas for $\alpha_{k}$ , $\gamma_{k}$ , and $\vec{p}_{k + 1}$ :

$\begin{array}{c} \displaystyle\alpha_{k} = \frac{\vec{r}_{k - 1}^{T}\vec{r}_{k - 1}}{\vec{p}_{k}A\vec{p}_{k}} \\[20pt] \displaystyle\gamma_{k} = \frac{\vec{r}_{k}^{T}\vec{r}_{k}}{\vec{r}_{k - 1}^{T}\vec{r}_{k - 1}} \\[28pt] \vec{p}_{k + 1} = \vec{r}_{k} + \gamma_{k}\vec{p}_{k}. \end{array}$

Proof.

The formula for $\vec{p}_{k + 1}$ comes from Lemma 6.

From Section 4d, we know that,

$\displaystyle\alpha_{k} = \frac{\vec{r}_{k - 1}^{T}\vec{p}_{k}}{\vec{p}_{k}^{T}A\vec{p}_{k}}, \,\,\,\,\,\,\gamma_{k} = -\frac{\vec{r}_{k}^{T}A\vec{p}_{k}}{\vec{p}_{k}^{T}A\vec{p}_{k}}, \,\,\,\,\,\,-A\vec{p}_{k} = \frac{\vec{r}_{k} - \vec{r}_{k - 1}}{\alpha_{k}}$ .

By orthogonality, the numerator of $\alpha_{k}$ simplifies to:

$\vec{r}_{k - 1}^{T}\vec{p}_{k} \,=\, \vec{r}_{k - 1}^{T}\vec{r}_{k - 1} + \gamma_{k - 1}\underbrace{\vec{r}_{k - 1}^{T}\vec{p}_{k - 1}}_{=\,0} \,=\, \vec{r}_{k - 1}^{T}\vec{r}_{k - 1}.$

As for $\gamma_{k}$ , note that,

$\displaystyle-\vec{r}_{k}^{T}A\vec{p}_{k} = \frac{\vec{r}_{k}^{T}\vec{r}_{k} - \vec{r}_{k}^{T}\vec{r}_{k - 1}}{\alpha_{k}} = \frac{\vec{r}_{k}^{T}\vec{r}_{k}}{\alpha_{k}}, \,\,\,\,\,\,\vec{p}_{k}^{T}A\vec{p}_{k} = \frac{\vec{r}_{k - 1}^{T}\vec{r}_{k - 1}}{\alpha_{k}}$ .

■

f. Summary

The pseudocode for CG looks like this:

% Initialize
x0 = zeros(n, 1), r0 = b, p1 = b;

for k = 1 : numIterations
    % Sparse matrix-vector multiply
    Ap1 = A * p1;

    % Find alpha
    alpha1 = (r0' * r0) / (p1' * Ap1);

    % Find the iterate
    x1 = x0 + alpha1 * p1;

    % Find the residual
    r1 = r0 - alpha1 * Ap1;

    % Find gamma
    gamma1 = (r1' * r1) / (r0' * r0);

    % Find the search direction
    p2 = r1 + gamma1 * p1;

    % Update the iterates
    x0 = x1;
    r0 = r1;
    p1 = p2;

end

Notice how we only need a sparse matrix-vector multiply, a vector-scalar multiply (axpy), and a dot product to solve a matrix equation. This is the power of iterative methods. We can make our code more efficient by reusing variables:

% Initialize
x = zeros(n, 1), r = b, p = b;
r_dot = r' * r;

for k = 1 : numIterations
    % Sparse matrix-vector multiply
    Ap = A * p;

    % Find alpha and initialize gamma
    alpha = r_dot / (p' * Ap);
    gamma = r_dot;

    % Find the iterate
    x = x + alpha * p;

    % Find the residual
    r = r - alpha * Ap;
    r_dot = r' * r;

    % Find gamma
    gamma = r_dot / gamma;

    % Find the search direction
    p = r + gamma * p;

end

5. Example

Let’s go back to 2D Poisson’s equation on a unit square domain, with homogeneous Dirichlet BC. Our RHS function is given by,

$f(x,\,y) = (a^{2} + b^{2})\pi^{2}\sin(a\pi x)\sin(b\pi y)$ ,

and we choose $a = 1$ , $b = 9$ , and $N = 200$ as before.

Stunningly, CG converges in 1 iteration! As far as iterative methods go, you can’t do better than that.

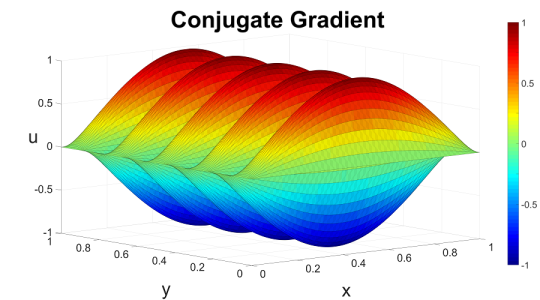
Graph of the CG solution — CG converges in 1 iteration!

The question is how? The RHS function that I chose makes the Poisson’s equation an eigenfunction problem. Even at the discrete level, the RHS vector $\vec{f}$ happens to be an eigenvector of $K$ :

$K\vec{f} = \lambda\vec{f}$ .

As a result, in the first iteration,

$\begin{array}{l} \displaystyle\alpha_{1} \,=\, \frac{\vec{f}^{T}\vec{f}}{\vec{f}^{T}K\vec{f}} \,=\, \frac{1}{\lambda} \\[20pt] \displaystyle\vec{r}_{1} \,=\, \vec{f} - \alpha_{1}K\vec{f} \,=\, \vec{f} - \frac{1}{\lambda} \cdot \lambda\vec{f} \,=\, \vec{0}. \end{array}$

Talk about luck (or well-planning)!

Notes

A big thanks goes to Dr. Ye, one of my teachers at Kentucky. He instilled my passion for numerical linear algebra and applications thereof. To learn additional iterative methods, I recommend reading his paper linked below.

You can find the code in its entirety here:

Download from GitHub

References

[1] Isaac Lee, lecture notes (2011).

[2] Qiang Ye, Deriving Optimal Krylov Subspace Methods.

[3] Qiang Ye, lecture notes (2009).

Iterative Methods: Part 3

4. Conjugate Gradient

a. Creating iterates

Lemma 1.

Proof.

b. Creating residuals

Lemma 2.

Proof.

Lemma 3.

Proof.

c. Creating search directions

Lemma 4.

Proof.

d. SPD

Lemma 5.

Proof.

Symmetric:

Bilinear:

Positive-definite:

e. Creating offshoots

Lemma 6.

Proof.

Lemma 7.

Proof.

f. Summary

5. Example

Notes

References

Leave a reply

4. Conjugate Gradient

a. Creating iterates

Lemma 1.

Proof.

b. Creating residuals

Lemma 2.

Proof.

Lemma 3.

Proof.

c. Creating search directions

Lemma 4.

Proof.

d. SPD

Lemma 5.

Proof.

Symmetric:

Bilinear:

Positive-definite:

e. Creating offshoots

Lemma 6.

Proof.

Lemma 7.

Proof.

f. Summary

5. Example

Notes

References

Share crunchingnumbers:

Leave a reply