I digitized my notes for advanced classes that I had enjoyed taking. Hope these may be of use to you.
Category: Blog posts
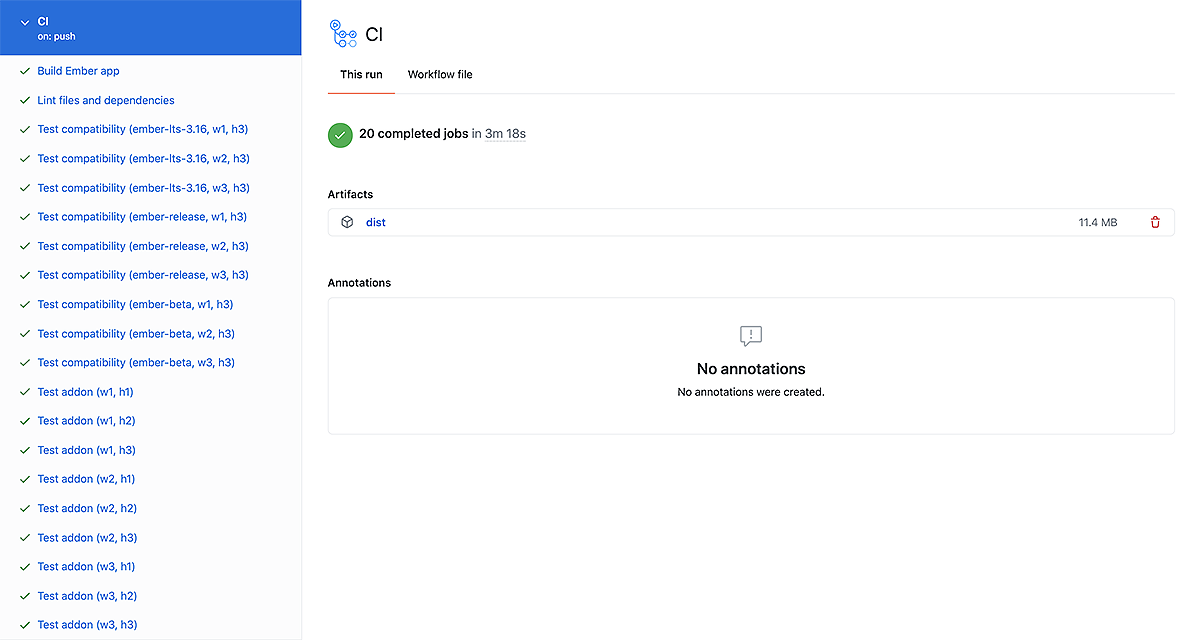
CI with GitHub Actions for Ember Apps: Part 2
2020 has been a tough, frail year. Last week, I joined many people who were laid off. Still I’m grateful for the good things that came out like Dreamland and CI with GitHub Actions for Ember Apps.
With GitHub Actions, I cut down CI runtimes for work projects to 3-4 minutes (with lower variance and more tests since March). I also noticed more and more Ember projects switching to GitHub Actions so I felt like a pioneer.
Today, I want to patch my original post and cover 3 new topics:
- How to migrate to v2 actions
- How to lower runtime cost
- How to continuously deploy (with ember-cli-deploy)
I will assume that you read Part 1 and are familiar with my workflow therein. Towards the end, you can find new workflow templates for Ember addons and apps.
Continue reading “CI with GitHub Actions for Ember Apps: Part 2”3 Refactoring Techniques
This mess was yours. Now your mess is mine.
Vance Joy
Hacktoberfest is coming up. If you’re new to open source contribution and unsure how to help, may I suggest refactoring code? You can provide a fresh perspective to unclear code and discover ways to leave it better than you found.
There are 3 refactoring techniques that I often practice:
- Rename things
- Remove nests
- Extract functions
Knowing how to apply just these 3 can get you far. I’ll explain what they mean and how I used them (or should have used them) in projects.
Continue reading “3 Refactoring Techniques”Container Queries: Cross-Resolution Testing
Failure to test is why I started to work on ember-container-query.
A few months ago, my team and I introduced ember-fill-up to our apps. It worked well but we noticed something strange. Percy snapshots that were taken at a mobile width would show ember-fill-up using the desktop breakpoint. They didn’t match what we were seeing on our browsers.
For a while, we ignored this issue because our CSS wasn’t great. We performed some tricks with flex and position that could have affected Percy snapshots. Guess what happened when we switched to grid and improved the document flow. We still saw incorrect Percy snapshots.
Container Queries: Adaptive Images
A powerful application of container queries is adaptive images. It’s about striking the balance between displaying an image that looks good (the larger the better) and one that loads fast (the smaller the better).
Currently, we are limited to srcset, which selects the optimal image based on the global screen size. This may work for splash images that cover the whole width, but what about images that we show in a partial area?
crunchingnumbers(a)live 
You must be logged in to post a comment.